


Here is a sample problem from electrical engineering using Kirchhoff’s Rules. Kirchhoff’s Rule states that the sum of the voltages in a loop must equal zero. (Where V = I*R) In the following diagram we know the voltages and resistances, and must determine the currents. We will end up with three equations, and three unknowns. We will solve for the three unknowns using Cramer’s Rule.
Below is an image of the example problem circuit.
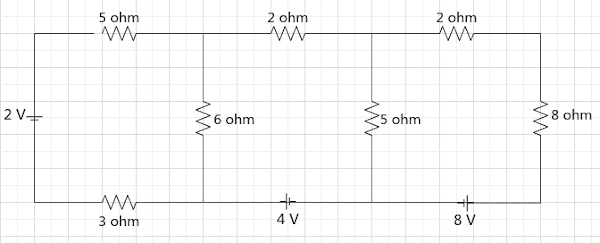
Here is the example problem circuit with the current loop unknowns.
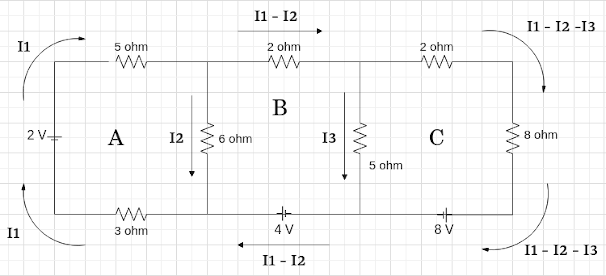
Here are the equations for each of the loops using V = I*R.
A: -5*I1 – 6*I2 – 3*I3 + 2 = 0We will use numpy to find four determinants. D, D1, D2, D3 From the four determinants we will get I1, I2, and I3.
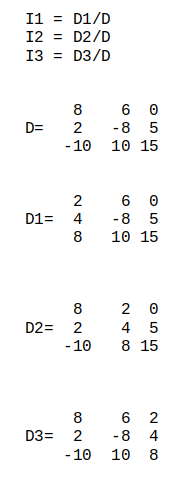
We will now write down the matrix for each determinant. We will then use the Python program to find the determinants and solve for I1, I2, I3.

The following is the Python code with the Output.
import numpy as np
a1=8
a2=6
a3=0
a=2
b1=2
b2=-8
b3=5
b=4
c1=-10
c2=10
c3=15
c=8
A = [[a1,a2,a3],[b1,b2,b3],[c1,c2,c3]]
A1 = [[a,a2,a3],[b,b2,b3],[c,c2,c3]]
A2 = [[a1,a,a3],[b1,b,b3],[c1,c,c3]]
A3 = [[a1,a2,a],[b1,b2,b],[c1,c2,c]]
D = np.linalg.det(A)
D1 = np.linalg.det(A1)
D2 = np.linalg.det(A2)
D3 = np.linalg.det(A3)
I1 = D1/D
I2 = D2/D
I3 = D3/D
print('I1 = ' , I1)
print('I2 = ' , I2)
print('I3 = ' , I3)
# Output
# I1 = 0.24999999999999994
# I2 = -0.0
# I3 = 0.6999999999999998
Notice that the code is not specific for this problem. It will work with any problem with three equations, and three unknowns. Note that this is the roundabout way to solve 3 equations with three unknowns. Numpy solve() is much quicker.
Table of Contents
Ch1-Install Python
Ch2-Install PyCharm
Ch3-Save Work
Ch4-Add Project
Ch5-Variables
Ch6-Print&Input
Ch7-Lists
Ch8-Loops
Ch9-If&Logical
Ch10-Functions
Ch11-Bubble Sort
Ch12-Plotting
Ch13-Files
Ch14-Print Format
Ch15-Dict&Comp&Zip
Ch16-Arrays
Ch17-Electrical
Ch18-Regression
Ch19-Differential
Ch20-Secant
