


We will use the secant program to solve a chemical engineering problem involving an equilibrium reaction.
This program finds the roots of a nonlinear equation using the secant method. The secant method always converges to a root provided that on a closed interval [a,b] given that f(a)*f(b)<0. Or, the function changes sign so the function must equal 0 on the interval.
The equation for the secant line is given by two points [x0,f(x0)] and [x1,f(x1)]. See the equation below.
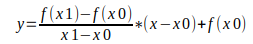
We will set y=0 and solve for x giving us:
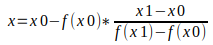
We will use the following general steps. The process is divided into two programs. The first indicates whether or not our first two guesses will work. The second uses the guesses to find the root using the secant method. The programs must be entered as separate files in PyCharm.
Run the first program as many times as necessary to find two acceptable guesses for x0, and x1. You must enter you function manually into code.
#FIRST PROGRAM
# Manually enter function from 20.4.1
def f(x):
p =3.5
k =.04
return k-x/(1-x)*(2*p/(2+x))**.5
#First Program - test input x0, x1
x0 = input('Input x0')
x1 = input('Input x1')
x0 = float(x0)
x1 = float(x1)
try0 = f(x0)
try1 = f(x1)
if f(x0) * f(x1) < 0:
print('The two numbers will work.')
else:
print('For x0 = ', x0, ' try0=', try0)
print('For x1 = ', x1, ' try1=', try1)
print('Rerun program with two new numbers.')
Run the second secant program. Manually enter the f(x) from 20.4.1, into code. Input x0, and x1 from 20.3.1, such that f(x0)*f(x1)<0. Input an acceptable error.
Use the program to compute x using the equation in 20.2.0, rewritten below in code.
x=x0-f(x0)*((x1-x0)/(f(x1)-f(x0))
In the next step we swap values of x0, and x1. Let x0 = x1, and x1 = x2 .
If abs(f(x2)) is greater than the acceptable error, perform the above calculation again. If the abs(f(x2) is smaller than the acceptable error, print the root, x2.
#SECOND PROGRAM
# Manually enter p, k, and f(x)
def f(x): #See 20.4.1 for p,k,f(x)
p = 3.5
k = .04
return k - x / (1 - x) * (2 * p / (2 + x)) ** .5
# Secant function
def secant(x0, x1, e):
iteration = 1
condition = True
while condition:
if f(x0) == f(x1):
print('Divide by zero error!')
break
x2 = x0 - (x1 - x0) * f(x0) / (f(x1) - f(x0))
print('Iteration-%d, x2 = %0.5f and f(x2) = %0.5f' % (iteration, x2, f(x2)))
x0 = x1
x1 = x2
iteration = iteration + 1
if iteration > 100:
print('More than 100 iterations.')
break
condition = abs(f(x2)) > e
print('The root is: ' , x2)
# Input Section - Second Program
x0 = input('Input x0 ')
x1 = input('Input x1 ')
e = input('Input allowable error')
# Convert x0 , x1, and e to float
x0 = float(x0)
x1 = float(x1)
e = float(e)
# Call secant function
secant(x0, x1, e)
Study the reaction where water vapor splits into hydrogen and oxygen at high temperatures and pressures.
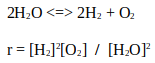
The following entities apply to the model:

Use the First Program and Second Program as shown above. Use the formula below, which is the code for the above formula. Try .5, and 0 for x0, and x1. The answer is m = 0.021 mole fraction of water vapor.
f(x) = k - x / (1 - x) * (2 * p / (2 + x)) ** .5
SALARSEN.COM
Table of Contents
Ch1-Install Python
Ch2-Install PyCharm
Ch3-Save Work
Ch4-Add Project
Ch5-Variables
Ch6-Print&Input
Ch7-Lists
Ch8-Loops
Ch9-If&Logical
Ch10-Functions
Ch11-Bubble Sort
Ch12-Plotting
Ch13-Files
Ch14-Print Format
Ch15-Dict&Comp&Zip
Ch16-Arrays
Ch17-Electrical
Ch18-Regression
Ch19-Differential
Ch20-Secant
